Este artigo fornece uma breve introdução às equações elementares e definições estatísticas mais comuns e fundamentais utilizadas na engenharia de confiabilidade e análise de dados de vida.
Variáveis aleatórias
Em geral, a maioria dos problemas da engenharia de confiabilidade lida com medidas quantitativas, como por exemplo o tempo até a falha de um componente, ou medidas qualitativas, como se um componente é defeituoso ou não defeituoso. Podemos então usar uma variável aleatória X para denotar essas medidas possíveis.
Entenda as diferenças entre defeito, falha e pane
No caso de tempos de falha, nossa variável aleatória X é o tempo de falha do componente e pode assumir um número infinito de valores possíveis em um intervalo de zero (0) a infinito (∞) (já que não sabemos o tempo exato a priori). Nosso componente pode ser encontrado com falha a qualquer momento após o tempo 0 (por exemplo, às 12 horas ou às 100 horas e assim por diante), assim X pode assumir qualquer valor neste intervalo. Neste caso, nossa variável aleatória X pode ser definida como uma variável aleatória contínua. Nesta referência, trataremos quase exclusivamente de variáveis aleatórias contínuas.
Ao determinar que um componente está defeituoso ou não defeituoso, apenas dois resultados são possíveis. Aquilo é, X é uma variável aleatória que pode assumir um de apenas dois valores (digamos defeituoso = 0 e não defeituoso = 1). Neste caso, diz-se que a variável é uma variável aleatória discreta.
A função de densidade de probabilidade e a função de distribuição cumulativa
A função de densidade de probabilidade (fdp) e a função de distribuição cumulativa (fdc) são duas das funções estatísticas mais importantes em confiabilidade e estão intimamente relacionadas. Quando essas funções são conhecidas, quase qualquer outra medida de confiabilidade de interesse pode ser derivada ou obtida. Vamos agora examinar mais de perto essas funções e como elas se relacionam com outras medidas de confiabilidade, como a função de confiabilidade e a taxa de falha.
De probabilidade e estatística, dada uma variável aleatória contínua X, denotamos:
- A função de densidade de probabilidade, fdp , como f( x ).
- A função de distribuição cumulativa, fdc , como F( x ).
A fdp e fdc fornecem uma descrição completa da distribuição de probabilidade de uma variável aleatória. A figura a seguir ilustra uma fdp:
As próximas figuras ilustram a relação fdp - fdc:
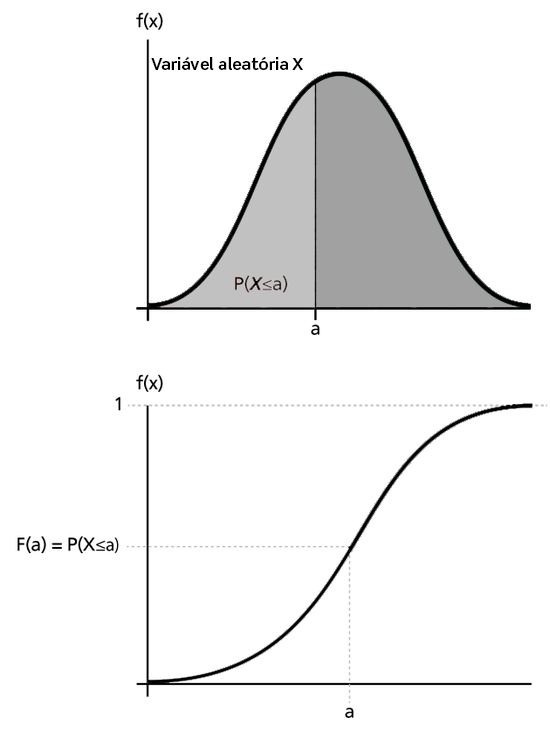
Se X é uma variável aleatória contínua, então a fdp de X é uma função, f(x), tal que para quaisquer dois números, a e b com a ≤ b:
Ou seja, a probabilidade de X assumir um valor no intervalo [a , b] é a área sob a função densidade de a para b, como mostrado acima. A fdp representa a frequência relativa dos tempos de falha em função do tempo.
A fdc é uma função, F( x ), de uma variável aleatória X, e é definido para um número x por:
Ou seja, para um número x, F( x ) é a probabilidade de que o valor observado de X será no máximo x. A fdc representa os valores acumulados da fdp. Ou seja, o valor de um ponto na curva da fdc representa a área sob a curva à esquerda desse ponto na fdp. Na confiabilidade, a fdc é utilizada para medir a probabilidade de o item em questão falhar, antes do valor de tempo associado, t, e também é chamada de não confiabilidade.
Curva PF: entenda o conceito e aplicação
Observe que, dependendo da função densidade, denotada por f( x ), os limites variam de acordo com a região na qual a distribuição é definida. Por exemplo, para as distribuições de vida consideradas nesta referência, com exceção da distribuição normal, esse intervalo seria [ 0 , + ∞ ].
Relação matemática: fdp e fdc
A relação matemática entre a fdp e a fdc é dada por:
Onde s é uma variável de integração fictícia.
Por outro lado:
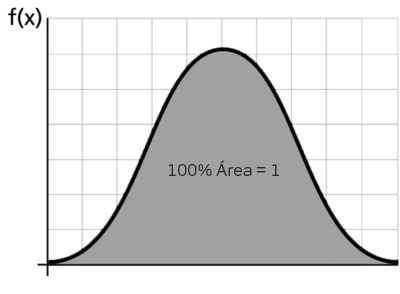
A fdc é a área sob a função densidade de probabilidade até um valor de x. A área total sob a fdp é sempre igual a 1, ou matematicamente:
A conhecida distribuição normal (ou gaussiana) é um exemplo de função de densidade de probabilidade. A fdp para esta distribuição é dada por:
Onde μ é a média e σ é o desvio padrão. A distribuição normal tem dois parâmetros, μ e σ.
Outra é a distribuição lognormal, cuja fdp é dada por:
Onde μ′ é a média dos logaritmos naturais dos tempos até a falha e σ′ é o desvio padrão dos logaritmos naturais dos tempos até a falha. Novamente, esta é uma distribuição de 2 parâmetros.
Função de confiabilidade
A função de confiabilidade pode ser derivada usando a definição anterior da função de distribuição cumulativa:
A partir da definição anterior da fdc, a probabilidade de um evento ocorrer no tempo t é dada por:
Ou, pode-se igualar este evento à probabilidade de uma unidade falhar pelo tempo t.
Como essa função define a probabilidade de falha em um determinado tempo, podemos considerá-la como a função de não confiabilidade. Subtrair essa probabilidade de 1 nos dará a função de confiabilidade, uma das funções mais importantes na análise de dados de vida. A função de confiabilidade fornece a probabilidade de sucesso de uma unidade realizar uma missão em um determinado intervalo de tempo. A figura a seguir ilustra isso.
Para mostrar isso matematicamente, primeiro definimos a função de não confiabilidade:
Que é a probabilidade de falha, ou a probabilidade de que nosso tempo de falha esteja na região de 0 e t. Este é o mesmo que a fdc . Então de
Confiabilidade e falta de confiabilidade são os dois únicos eventos considerados e são mutuamente exclusivos; portanto, a soma dessas probabilidades é igual à unidade.
Então:
Invesramente:
Função de confiabilidade condicional
A confiabilidade condicional é a probabilidade de completar com sucesso outra missão após a conclusão bem-sucedida de uma missão anterior. O tempo da missão anterior e o tempo da missão a ser realizada devem ser levados em consideração para os cálculos de confiabilidade condicional. A função de confiabilidade condicional é dada por:
Função de taxa de falha
A função de taxa de falhas permite determinar o número de falhas que ocorrem por unidade de tempo. Omitindo a derivação, a taxa de falha é matematicamente dada como:
Isso fornece a taxa de falha instantânea, também conhecida como função de risco. É útil para caracterizar o comportamento de falha de um componente, determinar a alocação da equipe de manutenção, planejar o fornecimento de peças sobressalentes, etc. A taxa de falha é indicada como falhas por unidade de tempo.
Vida média (MTTF)
A função de vida média, que fornece uma medida do tempo médio de operação até a falha, é dada por:
Este é o tempo médio até a falha esperado ou é indicado como o MTTF (Tempo Médio Até a Falha).
Saiba as diferenças entre MTTR, MTTF e MTBF
O MTTF, mesmo sendo um índice de desempenho de confiabilidade, não fornece nenhuma informação sobre a distribuição de falhas do componente em questão ao lidar com a maioria das distribuições de tempo de vida. Como distribuições muito diferentes podem ter meios idênticos, não é sensato usar o MTTF como a única medida da confiabilidade de um componente.
Vida mediana
Vida mediana, ou:
é o valor da variável aleatória que tem exatamente metade da área sob a fdp à sua esquerda e metade à sua direita. Representa o centróide da distribuição. A mediana é obtida resolvendo a seguinte equação para:
(Para dados individuais, a mediana é o valor do ponto médio.)
Vida modal (ou modo)
A vida modal (ou modo):
é o valor de T que satisfaz:
Para uma distribuição contínua, a moda é o valor de t que corresponde à densidade de probabilidade máxima (o valor no qual a fdp tem seu valor máximo, ou o pico da curva).
Distribuições vitalícias
Uma distribuição estatística é totalmente descrita por sua fdp. Nas seções anteriores, usamos a definição da fdp para mostrar como todas as outras funções mais comumente utilizadas na engenharia de confiabilidade e análise de dados de vida podem ser derivadas. A função de confiabilidade, função de taxa de falha, função de tempo médio e função de vida mediana podem ser determinadas diretamente a partir da definição de fdp, ou f(t). Existem diferentes distribuições, como a normal (Gaussiana), exponencial, Weibull e etc, e cada uma tem uma forma predefinida de f(t) que pode ser encontrada em muitas referências. De fato, existem algumas referências que se dedicam exclusivamente a diferentes tipos de distribuições estatísticas.
Baixe gratuitamente o ebook Curva da banheira
Essas distribuições foram formuladas por estatísticos, matemáticos e engenheiros para modelar matematicamente ou representar determinado comportamento. Por exemplo, a distribuição Weibull foi formulada por Waloddi Weibull e, portanto, leva seu nome. Algumas distribuições tendem a representar melhor os dados de vida e são mais comumente chamadas de "distribuições de vida".
Uma introdução mais detalhada sobre esse assunto será apresentada no artigo Distribuições de Vida.
| Traduzido e publicado sob licença Creative Commons |  |
ReliaWiki |
Caso encontre algo ofensivo que viole a legislação vigente no Brasil ou os termos de uso, DENUNCIE.
Fauzi Mendonça
APRESENTAÇÃO:
Fundador, Diretor Editorial e Colunista da Revista Manutenção, escreve regularmente sobre diversos assuntos relacionados ao cotidiano da Engenharia de Manutenção.
Desenvolvedor Web e Webdesigner, é responsável pelo design, layout, diagramação, identidade visual e logomarca da Revista Manutenção.
FORMAÇÃO ACADÊMICA E EXPERIÊNCIA PROFISSIONAL:Profissional graduado em Engenharia Eletrônica com ênfase em automação e controle industrial, pós graduado em Engenharia de Manutenção, pela Faculdade Anhanguera de Tecnologia (FAT) de São Bernardo, pós graduando do Curso de Engenharia de Confiabilidade, pela Universidade Tecnológica Federal do Paraná (UTFPR), atua há mais de quinze (15) anos com Planejamento e Controle de Manutenção (PCM), em empresas de médio e grande porte, nacionais e multinacionais, onde edificou carreira profissional como Programador, Planejador, Analista e Coordenador de PCM.
Acessar com Facebook
Acessar com Google
Acessar com Linkedin