Utilizamos o termo distribuições de vida para descrever a coleção de distribuições de probabilidade estatística, que empregamos em engenharia de confiabilidade e análise de dados de vida. Uma distribuição estatística é totalmente descrita por sua fdp (ou função de densidade de probabilidade). Nas seções anteriores, usamos a definição da fdp para mostrar como todas as outras funções mais comumente utilizadas em engenharia de confiabilidade e análise de dados de vida podem ser derivadas; ou seja, a função de confiabilidade, função de taxa de falha, função de tempo médio e função de vida média, etc. Tudo isso pode ser determinado diretamente a partir da definição da fdp , ou f(t). Existem diferentes distribuições, como a normal, exponencial, etc., e cada uma delas tem uma forma pré-definida de f(t). Essas definições de distribuição podem ser encontradas em muitas referências. Na verdade, textos inteiros foram dedicados à definição de famílias de distribuições estatísticas. Essas distribuições foram formuladas por estatísticos, matemáticos e engenheiros para modelar matematicamente ou representar determinado comportamento. Por exemplo, a distribuição Weibull foi formulada por Waloddi Weibull e, portanto, leva seu nome. Algumas distribuições tendem a representar melhor os dados de vida e são comumente chamadas de distribuições de vida. Uma das distribuições mais simples e mais comumente utilizadas (e muitas vezes erroneamente superutilizada devido à sua simplicidade) é a distribuição exponencial. A fdp da distribuição exponencial é matematicamente definida como:
Nesta definição, note que t é a nossa variável aleatória, que representa o tempo, e a letra grega λ (lambda) representa o que é comumente chamado de parâmetro da distribuição. Dependendo do valor de, λ, f(t) será escalado de forma diferente. Para qualquer distribuição, o parâmetro ou parâmetros da distribuição são estimados a partir dos dados. Por exemplo, a conhecida distribuição normal (ou gaussiana) é dada por:
μ, a média e σ, o desvio padrão, são seus parâmetros. Ambos os parâmetros são estimados a partir dos dados (ou seja, a média e o desvio padrão dos dados). Uma vez estimados esses parâmetros, nossa função f(t) está totalmente definido e podemos obter qualquer valor para f(t) dado qualquer valor de t.
Dada a representação matemática de uma distribuição, também podemos derivar todas as funções necessárias para a análise de dados de vida, que novamente dependerão apenas do valor de t após o valor do parâmetro ou parâmetros de distribuição ter sido estimado a partir dos dados. Por exemplo, sabemos que a distribuição exponencial fdp é dada por:
Assim, a função de confiabilidade exponencial pode ser derivada como:
A função de taxa de falha exponencial é:
O tempo médio até a falha exponencial (MTTF) é dado por:
Esta mesma metodologia pode ser aplicada a qualquer distribuição dada a sua fdp , com vários graus de dificuldade dependendo da complexidade do f(t).
Tipos de Parâmetros
As distribuições podem ter qualquer quantidade de parâmetros. Observe que, à medida que a quantidade de parâmetros aumenta, também aumenta a quantidade de dados necessários para um ajuste adequado. Em geral, as distribuições de tempo de vida utilizadas na confiabilidade e análise de dados de vida, geralmente são limitadas a um máximo de três parâmetros. Esses três parâmetros são geralmente conhecidos como parâmetro de escala, parâmetro de forma e parâmetro de localização.
Parâmetro de escala O parâmetro de escala é o tipo de parâmetro mais comum. Todas as distribuições nesta referência possuem um parâmetro de escala. No caso de distribuições de um parâmetro, o único parâmetro é o parâmetro de escala. O parâmetro de escala define onde está a maior parte da distribuição, ou quão estendida é a distribuição. No caso da distribuição normal, o parâmetro de escala é o desvio padrão.
Parâmetro de forma O parâmetro de forma, como o nome indica, ajuda a definir a forma de uma distribuição. Algumas distribuições, como a exponencial ou a normal, não possuem um parâmetro de forma, pois possuem uma forma predefinida que não muda. No caso da distribuição normal, a forma é sempre a familiar forma de sino. O efeito do parâmetro de forma em uma distribuição é refletido nas formas da fdp, a função de confiabilidade e a função de taxa de falhas.
Parâmetro de localização O parâmetro de localização é utilizado para deslocar uma distribuição em uma direção ou outra. O parâmetro de localização, geralmente denotado como xxx, define a localização da origem de uma distribuição e pode ser positiva ou negativa. Em termos de distribuições de tempo de vida, o parâmetro de localização representa uma mudança de tempo.
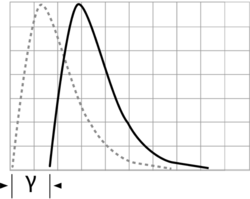
Isso significa que a inclusão de um parâmetro de localização para uma distribuição cujo domínio é normalmente[0,∞] vai mudar o domínio para [γ,∞], onde γ pode ser positivo ou negativo. Isso pode ter alguns efeitos profundos em termos de confiabilidade. Para um parâmetro de localização positivo, isso indica que a confiabilidade para essa distribuição específica é sempre 100% até esse ponto. Em outras palavras, uma falha não pode ocorrer antes desse tempo γ. Muitos engenheiros se sentem desconfortáveis em dizer que uma falha absolutamente não acontecerá antes de um determinado momento. Por outro lado, pode-se argumentar que quase todas as distribuições de vida têm um parâmetro de localização, embora muitas delas possam ser insignificantemente pequenas. Da mesma forma, muitas pessoas se sentem desconfortáveis com o conceito de um parâmetro de localização negativo, que afirma que as falhas ocorrem teoricamente antes do tempo zero. Realisticamente, o cálculo de um parâmetro de localização negativo é indicativo de falhas quiescentes (falhas que ocorrem antes de um produto ser utilizado pela primeira vez) ou de problemas com o processo de fabricação, embalagem ou envio. Mais atenção será dada ao conceito de parâmetro de localização em discussões subseqüentes das distribuições exponencial e Weibull.
Distribuições mais utilizadas
Existem muitas distribuições de tempo de vida diferentes que podem ser utilizadas para modelar dados de confiabilidade. Leemis[22] apresenta uma boa visão geral de muitas dessas distribuições. Nesta referência, vamos nos concentrar nas distribuições mais comumente utilizadas e mais amplamente aplicáveis para análise de dados de vida, conforme descrito nas seções a seguir.
A Distribuição Exponencial
A distribuição exponencial é comumente utilizadaa para componentes ou sistemas que exibem uma taxa de falha constante . Devido à sua simplicidade, tem sido amplamente utilizada, mesmo nos casos em que não se aplica. Em seu caso mais geral, a distribuição exponencial de 2 parâmetros é definida por:
Onde λ é a taxa de falha constante em falhas por unidade de medida (por exemplo, falhas por hora, por ciclo, etc.) e γ é o parâmetro de localização. Além disso:
onde m é o tempo médio entre falhas (ou até a falha).
Se o parâmetro de localização, γ, é assumido como zero, então a distribuição torna-se a exponencial de 1 parâmetro ou:
Para uma discussão detalhada dessa distribuição, consulte A distribuição exponencial.
A distribuição de Weibull
A distribuição Weibull é uma distribuição de confiabilidade de uso geral utilizada para modelar a resistência do material, tempos até a falha de componentes eletrônicos e mecânicos, equipamentos ou sistemas. Em seu caso mais geral, a FDP Weibull de 3 parâmetros é definida por:
onde β = parâmetro de forma, η = parâmetro de escala e γ = parâmetro de localização.
Se o parâmetro de localização, γ, é assumido como zero, então a distribuição mais apropriada é a Weibull de 2 parâmetros ou:
Uma forma adicional é a distribuição Weibull de 1 parâmetro, que assume que o parâmetro de localização, γ é zero, e o parâmetro de forma é uma constante conhecida, ou β = constante = ℂ, então:
Para uma discussão detalhada desta distribuição, veja A Distribuíção Weibull.
Análise Bayesiana-Weibull
Outra abordagem é o método de análise Weibull-Bayesiana, que assume que o analista possui algum conhecimento prévio sobre a distribuição do parâmetro de forma da distribuição Weibull (beta). Existem muitas aplicações práticas para este modelo, particularmente quando se lida com tamanhos de amostra pequenos e/ou quando algum conhecimento prévio do parâmetro de forma está disponível. Por exemplo, quando um teste é realizado, geralmente há um bom entendimento sobre o comportamento do modo de falha sob investigação, principalmente por meio de dados históricos ou física da falha.
Observe que isso não é o mesmo que o chamado "modelo WeiBayes", que é realmente uma distribuição Weibull de um parâmetro que assume um valor fixo (constante) para o parâmetro de forma e resolve para o parâmetro de escala. O recurso Bayesian-Weibull no Weibull++ é, na verdade, um verdadeiro modelo bayesiano e oferece uma alternativa ao Weibull de um parâmetro, incluindo a variação e a incerteza presentes na estimativa anterior do parâmetro de forma.
Este método de análise e suas características são apresentados em detalhes na Análise Bayesiana-Weibull.
A distribuição normal
A distribuição normal é comumente utilizadaa para análise de confiabilidade geral, tempos até a falha de componentes eletrônicos e mecânicos simples, equipamentos ou sistemas. A fdp da distribuição normal é dada por:
onde μ é a média dos tempos normais até a falha e σ é o desvio padrão dos tempos até a falha.
A distribuição normal e suas características são apresentadas em A distribuição normal.
A Distribuição Log-normal
A distribuição lognormal é comumente utilizadaa para análise de confiabilidade geral, ciclos até a falha em fadiga, resistência do material e variáveis de carregamento em projetos probabilísticos. Quando os logaritmos naturais dos tempos até a falha são normalmente distribuídos, dizemos que os dados seguem a distribuição lognormal.
A fdp da distribuição lognormal é dada por:
onde μ' é a média dos logaritmos naturais dos tempos até a falha e σ' é o desvio padrão dos logaritmos naturais dos tempos até a falha.
Para uma discussão detalhada dessa distribuição, consulte A Distribuíção Lognormal.
Outras distribuições
Além das distribuições mencionadas acima, que são utilizadaas com mais frequência na análise de dados de vida, as seguintes distribuições também têm uma variedade de aplicações e podem ser encontradas em muitas referências estatísticas. Elas estão incluídas no Weibull++, bem como são discutidas nesta referência.
A Distribuição Weibull Mista
A distribuição Weibull mista é comumente utilizadaa para modelar o comportamento de componentes ou sistemas que exibem modos de falha múltiplos (populações mistas). Dá uma visão global da vida de um produto misturando diferentes distribuições Weibull para diferentes estágios da vida do produto e é definida por:
onde o valor de S é igual ao número de subpopulações. Observe que isso resulta em um total de (3.S−1) parâmetros. Em outras palavras, cada população tem uma porção ou peso de mistura para oith população, um βi , ou parâmetro de forma para oith população e ou parâmetro de escala ηi para ith população. Observe que os parâmetros são reduzidos a(3⋅S−1), visto que a seguinte condição também pode ser utilizadaa:
A distribuição Weibull mista e suas características são apresentadas em A Distribuíção Weibull Mista.
A Distribuição Gama Generalizada
Em comparação com as outras distribuições discutidas anteriormente, a distribuição gama generalizada não é utilizadaa com tanta frequência para modelar dados de vida; no entanto, ele tem a capacidade de imitar os atributos de outras distribuições, como Weibull ou lognormal, com base nos valores dos parâmetros da distribuição. Isso oferece um compromisso entre duas distribuições de tempo de vida. A função gama generalizada é uma distribuição de três parâmetros com parâmetros μ, σ e λ. A fdp da distribuição é dada por:
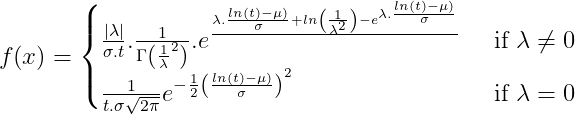
onde Γ(x) é a função gama, definida por:
Essa distribuição se comporta como outras distribuições com base nos valores dos parâmetros. Por exemplo, se λ=1, então a distribuição é idêntica à distribuição Weibull. Se ambos λ=1 e σ=1, então a distribuição é idêntica à distribuição exponencial, e para λ=0, é idêntica à distribuição lognormal. Embora a distribuição gama generalizada não seja frequentemente utilizada para modelar dados de vida por si só, sua capacidade de se comportar como outras distribuições de vida mais comumente utilizadaas às vezes é utilizadaa para determinar qual dessas distribuições de vida deve ser utilizadaa para modelar um determinado conjunto de dados.
A distribuição gama generalizada e suas características são apresentadas em A distribuição gama generalizada.
A Distribuição Gama
A distribuição gama é uma distribuição flexível que pode oferecer um bom ajuste para alguns conjuntos de dados de vida. Às vezes chamada de distribuição Erlang, a distribuição gama tem aplicações na análise bayesiana como uma distribuição a priori e também é comumente usada na teoria das filas.
A fdp da distribuição gama é dada por:
onde:
μ = Parâmetro de escala
k = Parâmetro de forma
onde 0 < t < ∞, −∞ < μ < ∞ e k > 0.
A distribuição gama e suas características são apresentadas em A Distribuíção Gama.
A Distribuição Logística
A distribuição logística tem uma forma muito semelhante à distribuição normal (ou seja, em forma de sino), mas com caudas mais pesadas. Uma vez que a distribuição logística tem soluções de forma fechada para as funções de confiabilidade, cdf e taxa de falhas, às vezes é preferível à distribuição normal, onde essas funções só podem ser obtidas numericamente.
A fdp da distribuição logística é dada por:
onde:
μ = Parâmetro de localização (Também denotado como T)
σ = Parâmetro de escala
A distribuição logística e suas características são apresentadas em A Distribuição Logística.
A Distribuição Loglogística
Como pode ser deduzido através do nome, a distribuição loglogística é semelhante à distribuição logística. Especificamente, os dados seguem uma distribuição loglogística quando os logaritmos naturais dos tempos até a falha seguem uma distribuição logística. Consequentemente, as distribuições loglogística e lognormal também compartilham muitas semelhanças.
A fdp da distribuição loglogistica é dada por:
onde:
μ = Parâmetro de escala
σ = Parâmetro de forma
A distribuição loglogística e suas características são apresentadas em A distribuição loglogística.
A distribuição de Gumbel
A distribuição de Gumbel também é chamada de distribuição de menor valor extremo (MVE) ou distribuição de menor valor extremo (tipo 1). A distribuição de Gumbel é apropriada para modelar a resistência, que às vezes é desviada para a esquerda (por exemplo, poucas unidades fracas falham sob baixa tensão, enquanto o restante falha em tensões mais altas). A distribuição Gumbel também pode ser apropriada para modelar a vida útil de produtos que sofrem desgaste muito rápido após atingir uma certa idade.
A fdp da distribuição de Gumbel é dada por:
onde:
μ = Parâmetro de localização
σ = Parâmetro de escala
A distribuição Gumbel e suas características são apresentadas em A Distribuíção de Gumbel (MVE).
Referências bibliográficas
22. Leemis, Lawrence M., Reliability - Probabilistic Models and Statistical Methods, Prentice Hall, Inc., Englewood Cliffs, New Jersey, 1995.
| Traduzido e publicado sob licença Creative Commons |  |
ReliaWiki |


